json-api-normalizer: An Easy Way To Integrate The JSON API And Redux
As a front-end developer, for each and every application I work on, I need to decide how to manage the data. The problem can be broken down into the following three subproblems:
- fetch data from the back end,
- store it somewhere locally in the front-end application,
- retrieve the data from the local store and format it as required by the particular view or screen.
This article sums up my experience with consuming data from JSON, the JSON API and GraphQL back ends, and it gives practical recommendations on how to manage front-end application data.
Creating Secure Password Resets With JSON Web Tokens
Does your site still send password reminders via email? This should be a red flag to you, both as a user and a developer. Let’s look into how to create secure password resets with JSON web tokens. Read a related article →
To illustrate my ideas and make the article closer to real-world use cases, I’ll develop a very simple front-end application by the end of the article. Imagine we’ve implemented a survey that asks the same pile of questions of many users. After each user has provided their answers, other users may comment on them if desired. Our web app will perform a request to the back end, store the fetched data in the local store and render the content on the page. To keep things simple, we will omit the answer-creation flow.

A live demo is also available on GitHub
Back Story
In the last couple of years, I’ve participated in many front-end projects based on the React stack. We use Redux to manage state not only because it is the most widely used solution in its category, according to the recent State of JavaScript in 2016 survey, but it is also very lightweight, straightforward and predictable. Yes, sometimes it requires a lot more boilerplate code to be written than other state-management solutions; nevertheless, you can fully understand and control how your application works, which gives you a lot of freedom to implement any business logic and scenarios.
To give you some context, some time ago we tried GraphQL and Relay in one of our proofs of concept. Don’t get me wrong: It worked great. However, every time we wanted to implement a flow that was slightly different from the standard one, we ended up fighting with our stack, instead of delivering new features. I know that many things have changed since then, and Relay is a decent solution now, but we learned the hard way that using simple and predictable tools works better for us because we can plan our development process more precisely and better meet our deadlines.
Note: Before moving forward, I assume that you have some basic knowledge of state management and either Flux or Redux.
Redux Best Practices
The best thing about Redux is that it is unopinionated about what kind of API you consume. You can even change your API from JSON to JSON API or GraphQL and back during development, and as long as you preserve your data model, it will not affect the implementation of your state management at all. This is possible because, before you send the API response to the store, you would process it in a certain way. Redux itself doesn’t force you to do that; however, the community has identified and developed several best practices based on real-world experience. Following these practices will save you a lot of time by reducing the complexity of your applications and decreasing the number of bugs and edge cases.
Best Practice 1: Keep Data Flat In The Redux Store
Let’s go back to the demo application and discuss the data model:
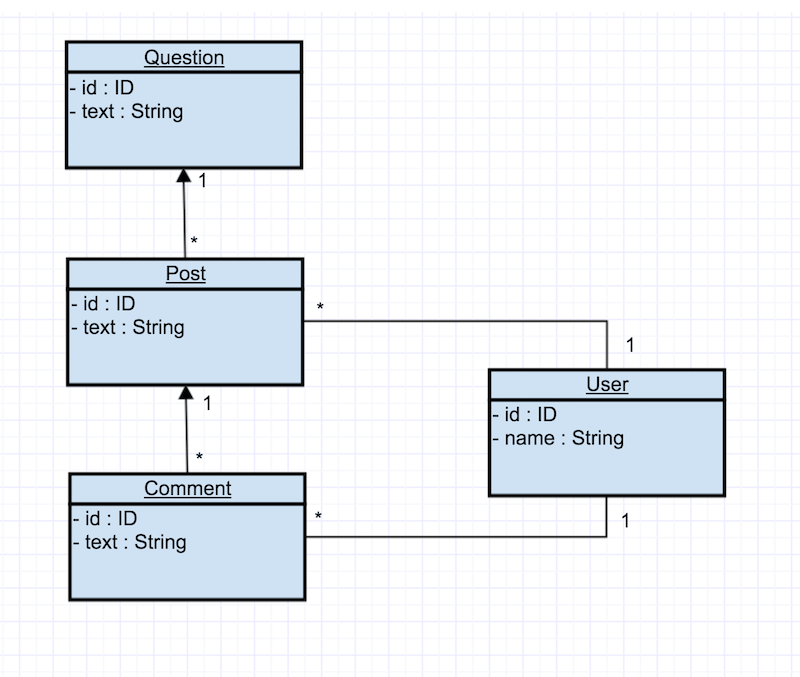
Here we have a question data object, which might have many post objects. Each post might have many comment objects. Each post and comment has one author, respectively.
Let’s assume we have a back end that returns a typical JSON response. Very likely it would have a deeply nested structure. If you prefer to store your data in a similar manner in the store, you will sooner or later face many issues. For example, you might store the same object several times. You might have post and comment objects that share the same author. Your store would look like this:
{
"text": "My Post",
"author": {
"name": "Yury",
"avatar": "avatar1.png"
},
"comments": [
{
"text": "Awesome Comment",
"author": {
"name": "Yury",
"avatar": "avatar1.png"
}
}
]
}
As you can see, we store the same Authorobject in several places, which not only requires more memory but also has negative side effects. Imagine if in the back end somebody changed the user’s avatar. Instead of updating one object in the Redux store, you would now need to traverse the whole state and update all instances of the same object. Not only might it be very slow, but it would also require you to learn precisely the data object’s structure.
Refactoring would be a nightmare as well. Another issue is that if you decided to reuse certain data objects for new views and they were nested in some other objects, then traversal implementation would be complex, slow and dirty.
Instead, we can store the data in a flattened structure. This way, each object would be stored only once, and we would have very easy access to any data.
{
"post": [{
"id": 1,
"text": "My Post",
"author": { "id": 1 },
"comments": [ { "id": 1 } ]
}],
"comment": [{
"id": 1,
"text": "Awesome Comment"
}],
"author": [{
"name": "Yury",
"avatar": "avatar1.png",
"id": 1
}]
}
The same principles have been widely used in relational database management systems for many years.
2. Store Collections As Maps Whenever Possible
OK, so we’ve got the data in a nice flat structure. It is a very common practice to incrementally accumulate received data, so that we can reuse it later as a cache, to improve performance or for offline use.
However, after merging new data in the existing storage, we need to select only relevant data objects for the particular view, not everything we’ve received so far. To achieve this, we can store the structure of each JSON document separately, so that we can quickly figure out which data objects were provided in a particular request. This structure would contain a list of the data object IDs, which we could use to fetch the data from the storage.
Let me illustrate this point. We will perform two requests to fetch a list of friends of two different users, Alice and Bob, and review the contents of our storage accordingly. To make things easier, let’s assume that, in the beginning, the storage is empty.
/alice/friends Response
So, here we are getting the User data object with an ID of 1 and a name of Mike, which might be stored like this:
{
"data": [{
"type": "User",
"id": "1",
"attributes": {
"name": "Mike"
}
}]
}
/bob/friends Response
Another request would return a User with the ID of 2 and the name of Kevin:
{
"data": [{
"type": "User",
"id": "2",
"attributes": {
"name": "Kevin"
}
}]
}
Storage State
After merging, our storage would look like this:
{
"users": [
{
"id": "1",
"name": "Mike"
},
{
"id": "2",
"name": "Kevin"
}
]
}
The big question is, how can we distinguish from this point on which users are Alice’s friends and which are Bob’s?
Storage State With Meta Data
We could preserve the structure of the JSON API document, so that we might quickly figure out which data objects in storage are relevant. Keeping this in mind, we could change the implementation of the storage so that it looks like this:
{
"users": [
{
"id": "1",
"name": "Mike"
},
{
"id": "2",
"name": "Kevin"
}
],
"meta": {
"/alice/friends": [
{
"type": "User",
"id": "1"
}
],
"/bob/friends": [
{
"type": "User",
"id": "2"
}
]
}
}
Now, we can read the meta data and fetch all mentioned data objects. Problem solved! Can we do better? Note that we are constantly doing three operations: insert, read and merge. Which data structure will perform best for us?
Let’s briefly recap the operation’s complexities.
| Type | Add | Delete | Search | Preserves Order |
|---|---|---|---|---|
| Map | O(1) | O(1) | O(1) | No |
| Array | O(1) | O(n) | O(n) | Yes |
Note: If you are not familiar with Big O notation, n here means the number of data objects, O(1) means that the operation will take relatively the same amount of time regardless of the data set size, and O(n) means that the operation’s execution time is linearly dependent on the data set’s size.
As we can see, maps will work a lot better than arrays because all operations have a complexity of O(1), instead of O(n). If the order of data objects is important, we still can use maps for data handling and save the ordering information in the meta data. Maps can also be easily transformed into arrays and sorted, if required.
Let’s reimplement the storage mentioned above and use a map instead of an array for the User data object.
Storage State Revised
{
"users": {
"1": {
"name": "Mike"
},
"2": {
"name": "Kevin"
}
},
"meta": {
"/alice/friends": [
{
"type": "User",
"id": "1"
}
],
"/bob/friends": [
{
"type": "User",
"id": "2"
}
]
}
}
Now, instead of iterating over the whole array to find a particular user, we can get it by ID almost instantly.
Processing The Data And JSON API
As you can imagine, there should be a widely used solution to convert JSON documents to a Redux-friendly form. The Normalizr library was initially developed by Dan Abramov, the author of Redux, for this purpose. You have to provide a JSON document and the scheme to “normalize” the function, and it will return the data in a nice flat structure, which we can save in the Redux store.
We’ve used this approach in many projects, and while it works great if your data model is known in advance and won’t change much within the application’s lifecycle, it dramatically fails if things are too dynamic. For example, when you are prototyping, developing a proof of concept or creating a new product, the data model will change very frequently to fit new requirements and change requests. Each back-end change should be reflected in an update to the Normalizr scheme. Because of this, several times I ended up fighting with my front-end app to fix things, rather than working on new features.
Are there any alternatives? We tried out GraphQL and the JSON API.
While GraphQL seems very promising and might be an interesting choice, we were not able to adopt it at the time because our APIs were being consumed by many third parties, and we couldn’t just drop the REST approach.
Let’s briefly discuss the JSON API standard.
JSON API Vs. Typical Web Services
Here are the JSON API’s main features:
- Data is represented in a flat structure, with relationships no more than one level deep.
- Data objects are typified.
- The specification defines pagination, sorting and data-filtering features out of the box.
A Typical JSON Document
{
"id": "123",
"author": {
"id": "1",
"name": "Paul"
},
"title": "My awesome blog post",
"comments": [
{
"id": "324",
"text": "Great job, bro!",
"commenter": {
"id": "2",
"name": "Nicole"
}
}
]
}
JSON API Document
{
"data": [{
"type": "post",
"id": "123",
"attributes": {
"id": 123,
"title": "My awesome blog post"
},
"relationships": {
"author": {
"type": "user",
"id": "1"
},
"comments": {
"type": "comment",
"id": "324"
}
}
}],
"included": [{
"type": "user",
"id": "1",
"attributes": {
"id": 1,
"name": "Paul"
}
}, {
"type": "user",
"id": "2",
"attributes": {
"id": 2,
"name": "Nicole"
}
}, {
"type": "comment",
"id": "324",
"attributes": {
"id": 324,
"text": "Great job!"
},
"relationships": {
"commenter": {
"type": "user",
"id": "2"
}
}
}]
}
The JSON API might seem too verbose compared to traditional JSON, right?
| Type | Raw (bytes) | Gzipped (bytes) |
|---|---|---|
| Typical JSON | 264 | 170 |
| JSON API | 771 | 293 |
While the raw size difference might be remarkable, the Gzipped sizes are much closer to each other.
Keep in mind that it is also possible to develop a contrived example whose size in a typical JSON format is greater than that of the JSON API. Imagine dozens of blog posts that share the same author. In a typical JSON document, you would have to store the author object for each post object, whereas in the JSON API format, the author object would be stored only once.
The bottom line is, yes, the size of JSON API document on average is bigger, but it shouldn’t be considered an issue. Typically, you will be dealing with structured data, which compresses to one fifth in size or more and which is also relatively small thanks to pagination.
Let’s discuss the advantages:
- First of all, the JSON API returns data in a flat form, with no more than one level of relationships. This helps to avoid redundancy and guarantees that each unique object will be stored in a document only once. This approach is a perfect match for Redux best practices, and we will use this feature soon.
- Secondly, data is provided in the form of typified objects, which means that on the client side you don’t need to implement parsers or define schemes like you do with Normalizr. This will make your front-end apps more flexible to changes in data structure and will require less effort on your side to adapt the application to new requirements.
- Thirdly, the JSON API specification defines a
linksobject, which helps with moving pagination and with filtering and sorting features from your application to JSON API clients. An optionalmetaobject is also available, where you can define your app-specific payload.
JSON API And Redux
Redux and the JSON API work great when used together; they complement each other well.
The JSON API provides data in a flat structure by definition, which conforms nicely with Redux best practices. Data comes typified, so that it can be naturally saved in Redux’s storage in a map with the format type → map of objects.
So, are we missing anything?
Despite the fact that dividing data objects into two types, “data” and “included,” might make some sense for the application, we can’t afford to store them as two separate entities in the Redux store, because then the same data objects would be stored more than once, which violates Redux best practiсes.
As we discussed, the JSON API also returns a collection of objects in the form of an array, but for the Redux store, using a map is a lot more suitable.
To resolve these issues, consider using my json-api-normalizer library.
Here are the main features of json-api-normalizer:
- Merge data and included fields, normalizing the data.
- Collections are converted into maps in a form a
id=>object. - The response’s original structure is stored in a special
metaobject
First of all, a distinction between data and included data objects was introduced in the JSON API specification, to resolve issues with recursive structures and circular dependencies. Secondly, most of the time, data in Redux is incrementally updated, which helps to improve performance, and it has offline support. However, as we work with the same data objects in our application, sometimes it is not possible to distinguish which data objects we should use for a particular view. json-api-normalizer can store a web service response’s structure in a special meta field, so that you can unambiguously determine which data objects were fetched for a particular API request.
Implementing The Demo App
Note: I assume that you have some practical experience with React and Redux.
Once again, we will build a very simple web app that will render the survey data provided by the back end in JSON API format.
We will start with the boilerplate, which has everything we need for the basic React app; we will implement Redux middleware to process the JSON API documents; we’ll provide the reducers data in an appropriate format; and we’ll build a simple UI on top of that.
First of all, we need a back end with JSON API support. Because this article is fully dedicated to front-end development, I’ve prebuilt a publicly available data source, so that we can focus on our web app. If you are interested, you can check the source code. Note that many JSON API implementation libraries are available for all kinds of technology stacks, so choose the one that works best for you.
My demo web service gives us two questions. The first one has two answers, and the second has three. The second answer to the first question has three comments.
The web service’s output will be converted to something similar to Heroku’s example after the user presses the button and the data is successfully fetched.
1. Download The Boilerplate
To reduce time in configuring the web app, I’ve developed a small React boilerplate that can be used as a starting point.
Let’s clone the repository.
git clone https://github.com/yury-dymov/json-api-react-redux-example.git --branch initial
Now we have the following:
- React and ReactDOM;
- Redux and Redux DevTools;
- Webpack;
- ESLint;
- Babel;
- an entry point to the application, two simple components, ESLint configuration, Webpack configuration and Redux store initialization;
- definition CSS for all components, which we are going to develop;
Everything should work out of the box, with no action needed on your part.
To start the application, type this in the console:
npm run webpack-dev-server
Then, open https://localhost:8050 in a browser.
2. API Integration
Let’s start with developing Redux middleware that will interact with API. We will use json-api-normalizer here to adhere to the don’t-repeat-yourself (DRY) principle; otherwise, we would have to use it over and over again in many Redux actions.
src/redux/middleware/api.js
import fetch from 'isomorphic-fetch';
import normalize from 'json-api-normalizer';
const API_ROOT = 'https://phoenix-json-api-example.herokuapp.com/api';
export const API_DATA_REQUEST = 'API_DATA_REQUEST';
export const API_DATA_SUCCESS = 'API_DATA_SUCCESS';
export const API_DATA_FAILURE = 'API_DATA_FAILURE';
function callApi(endpoint, options = {}) {
const fullUrl = (endpoint.indexOf(API_ROOT) === -1) ? API_ROOT + endpoint : endpoint;
return fetch(fullUrl, options)
.then(response => response.json()
.then((json) => {
if (!response.ok) {
return Promise.reject(json);
}
return Object.assign({}, normalize(json, { endpoint }));
}),
);
}
export const CALL_API = Symbol('Call API');
export default function (store) {
return function nxt(next) {
return function call(action) {
const callAPI = action[CALL_API];
if (typeof callAPI === 'undefined') {
return next(action);
}
let { endpoint } = callAPI;
const { options } = callAPI;
if (typeof endpoint === 'function') {
endpoint = endpoint(store.getState());
}
if (typeof endpoint !== 'string') {
throw new Error('Specify a string endpoint URL.');
}
const actionWith = (data) => {
const finalAction = Object.assign({}, action, data);
delete finalAction[CALL_API];
return finalAction;
};
next(actionWith({ type: API_DATA_REQUEST, endpoint }));
return callApi(endpoint, options || {})
.then(
response => next(actionWith({ response, type: API_DATA_SUCCESS, endpoint })),
error => next(actionWith({ type: API_DATA_FAILURE, error: error.message || 'Something bad happened' })),
);
};
};
}
Once the data is returned from the API and parsed, we can convert it to a Redux-friendly format with json-api-normalizer and forward it to the Redux actions.
Note: This code was copied and pasted from a real-world Redux instance, with small adjustments to add json-api-normalizer. Now you can see that integration with json-api-normalizer is simple and straightforward.
src/redux/configureStore.js
Let’s adjust the Redux store’s configuration:
+++ import api from './middleware/api';
export default function (initialState = {}) {
const store = createStore(rootReducer, initialState, compose(
--- applyMiddleware(thunk),
+++ applyMiddleware(thunk, api),
DevTools.instrument(),
src/redux/actions/post.js
Now we can implement our first action, which will request data from the back end:
import { CALL_API } from '../middleware/api';
export function test() {
return {
[CALL_API]: {
endpoint: '/test',
},
};
}
src/redux/reducers/data.js
Let’s implement the reducer, which will merge the data provided from the back end into the Redux store:
import merge from 'lodash/merge';
import { API_DATA_REQUEST, API_DATA_SUCCESS } from '../middleware/api';
const initialState = {
meta: {},
};
export default function (state = initialState, action) {
switch (action.type) {
case API_DATA_SUCCESS:
return merge(
{},
state,
merge({}, action.response, { meta: { [action.endpoint]: { loading: false } } }),
);
case API_DATA_REQUEST:
return merge({}, state, { meta: { [action.endpoint]: { loading: true } } });
default:
return state;
}
}
src/redux/reducers/data.js
Now we need to add our reducer to the root reducer:
import { combineReducers } from 'redux';
import data from './data';
export default combineReducers({
data,
});
src/components/Content.jsx
The model layer is done! Let’s add the button that will trigger the fetchData action and download some data for our app.
import React, { PropTypes } from 'react';
import { connect } from 'react-redux';
import Button from 'react-bootstrap-button-loader';
import { test } from '../../redux/actions/test';
const propTypes = {
dispatch: PropTypes.func.isRequired,
loading: PropTypes.bool,
};
function Content({ loading = false, dispatch }) {
function fetchData() {
dispatch(test());
}
return (
<div>
<Button loading={loading} onClick={() => { fetchData(); }}>Fetch Data from API</Button>
</div>
);
}
Content.propTypes = propTypes;
function mapStateToProps() {
return {};
}
export default connect(mapStateToProps)(Content);
Let’s open our page in a browser. With the help of our browser’s developer tools and Redux DevTools, we can see that the application is fetching the data from the back end in JSON API document format, converts it to a more suitable representation and stores it in the Redux store. Great! Everything works as expected. So, let’s add some UI components to visualize the data.
3. Fetching The Data From The Store
The redux-object package converts the data from the Redux store into a JSON object. We need to pass part of the store, the object type and the ID, and it will take care of the rest.
import build, { fetchFromMeta } from 'redux-object';
console.log(build(state.data, 'post', '1')); // ---> Post Object: { text: "I am fine", id: 1, author: @AuthorObject }
console.log(fetchFromMeta(state.data, '/posts')); // ---> array of posts
All relationships are represented as JavaScript object properties, with lazy-loading support. So, all child objects will be loaded only when required.
const post = build(state.data, 'post', '1'); // ---> post object; `author` and `comments` properties are not loaded yet
post.author; // ---> User Object: { name: "Alice", id: 1 }
Let’s add several UI components to visualize the data.
Typically, React’s component structure follows the data model, and our app is no exception.
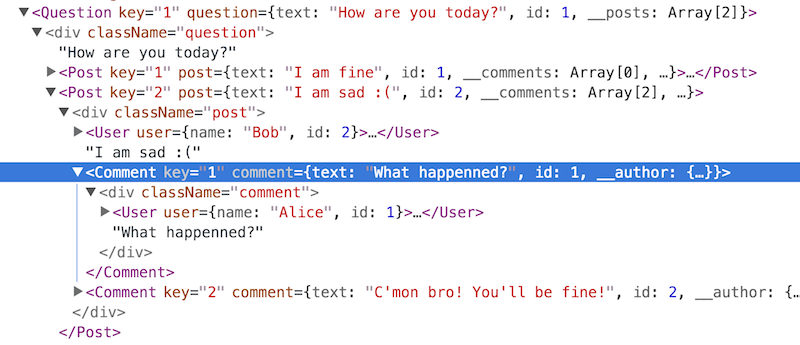
src/components/Content.jsx
First, we need to fetch the data from the store and propogate it to the component via the connect function from react-redux:
import React, { PropTypes } from 'react';
import { connect } from 'react-redux';
import Button from 'react-bootstrap-button-loader';
import build from 'redux-object';
import { test } from '../../redux/actions/test';
import Question from '../Question';
const propTypes = {
dispatch: PropTypes.func.isRequired,
questions: PropTypes.array.isRequired,
loading: PropTypes.bool,
};
function Content({ loading = false, dispatch, questions }) {
function fetchData() {
dispatch(test());
}
const qWidgets = questions.map(q => <Question key={q.id} question={q} />);
return (
<div>
<Button loading={loading} onClick={() => { fetchData(); }}>Fetch Data from API</Button>
{qWidgets}
</div>
);
}
Content.propTypes = propTypes;
function mapStateToProps(state) {
if (state.data.meta['/test']) {
const questions = (state.data.meta['/test'].data || []).map(object => build(state.data, 'question', object.id));
const loading = state.data.meta['/test'].loading;
return { questions, loading };
}
return { questions: [] };
}
export default connect(mapStateToProps)(Content);
We are fetching object IDs from the meta data of the API request with the /test endpoint, building JavaScript objects with the redux-object library and providing them to our component in the questions prop.
Now we need to implement a bunch of “dumb” components for rendering questions, posts, comments and users. They are very straightforward.
src/components/Question/package.json
Here is the package.json of the Question visualization component:
{
"name": "question",
"version": "0.0.0",
"private": true,
"main": "./Question"
}
src/components/Question/Question.jsx
The Question component renders the question text and the list of answers.
import React, { PropTypes } from 'react';
import Post from '../Post';
const propTypes = {
question: PropTypes.object.isRequired,
};
function Question({ question }) {
const postWidgets = question.posts.map(post => <Post key={post.id} post={post} />);
return (
<div className="question">
{question.text}
{postWidgets}
</div>
);
}
Question.propTypes = propTypes;
export default Question;
src/components/Post/package.json
Here is the package.json of the Post component:
{
"name": "post",
"version": "0.0.0",
"private": true,
"main": "./Post"
}
src/components/Post/Post.jsx
The Post component renders some information about the author, the answer text and also the list of comments.
import React, { PropTypes } from 'react';
import Comment from '../Comment';
import User from '../User';
const propTypes = {
post: PropTypes.object.isRequired,
};
function Post({ post }) {
const commentWidgets = post.comments.map(c => <Comment key={c.id} comment={c} />);
return (
<div className="post">
<User user={post.author} />
{post.text}
{commentWidgets}
</div>
);
}
Post.propTypes = propTypes;
export default Post;
src/components/User/package.json
Here is the package.json of the User component:
{
"name": "user",
"version": "0.0.0",
"private": true,
"main": "./User"
}
src/components/User/User.jsx
The User component renders some meaningful information about either the answer or the comment’s author. In this app, we will output just the user’s name, but in a real application, we could add an avatar and other nice things for a better user experience.
import React, { PropTypes } from 'react';
const propTypes = {
user: PropTypes.object.isRequired,
};
function User({ user }) {
return <span className="user">{user.name}: </span>;
}
User.propTypes = propTypes;
export default User;
src/components/Comment/package.json
Here is the package.json of the Comment component:
{
"name": "comment",
"version": "0.0.0",
"private": true,
"main": "./Comment"
}
src/components/Comment/Comment.jsx
The Comment component is very similar to the Post component. It renders some information about the author and the comment’s text.
import React, { PropTypes } from 'react';
import User from '../User';
const propTypes = {
comment: PropTypes.object.isRequired,
};
function Comment({ comment }) {
return (
<div className="comment">
<User user={comment.author} />
{comment.text}
</div>
);
}
Comment.propTypes = propTypes;
export default Comment;
And we are done! Open the browser, press the button, and enjoy the result.
If something doesn't work for you, feel free to compare your code with my project’s master branch
A live demo is also available on GitHub.
Conclusion
This ends the story I would like to tell. This approach helps us to prototype a lot faster and to be very flexible with changes to the data model. Because data comes out typified and in a flat structure from the back end, we don't need to know in advance the relationships between data objects and particular fields. Data will be saved in the Redux store in a format that conforms to the Redux best practices anyway. This frees us to dedicate most of our time to developing features and experimenting, rather than adopting normalizr schemes, rethinking selectors and debugging over and over again.
I encourage you to try the JSON API in your next pet project. You’ll spend more time on experiments, without fear of breaking things.
Related Links
- JSON API specification
- “Implementations,” JSON API
- json-api-normalizer, Yury Dymov, GitHub
- redux-object, Yury Dymov, GitHub
- Phoenix JSON API Example, Yury Dymov, GitHub
JSON API data source example source code - json-api-normalizer Demo, Yury Dymov, GitHub
A React application consuming a JSON API live demo - JSON API React Redux Example, Yury Dymov, GitHub
React application source code, initial version - JSON API React Redux Example, Yury Dymov, GitHub
React application source code, final version
Further Reading
- SolidStart: A Different Breed Of Meta-Framework
- Making Sense Of “Senseless” JavaScript Features
- A Guide To Redux Toolkit With TypeScript
- Generating Real-Time Audio Sentiment Analysis With AI








